標準偏差から見た長期投資の優位性

ここをお読みになる前に、正規分布と標準偏差をお読みください。
ここでは、標準偏差についてもう少し突っ込んだ議論をしながら、なぜ、長期投資が有利なのかについて考察してみましょう。

リターンと標準偏差の計算

さて、リスクのところで述べたように、標準偏差は分散の平方根です。
分散は、毎月のファンドの騰落率と騰落率の平均値の差（偏差）の2乗を足し合わせて、データの数で割れば分散が得られます。（月次分散）
月次分散の平方根を計算すると月次標準偏差が得られるわけです｡

2006年2月末時点で、ちょうど12個のデータがあるファンドがあります。

FPI_P43 Invesco GT Capital Shield (USD)

Date	月次騰落率(%)
2006-2	0.50
2006-1	0.71
2005-12	1.12
2005-11	2.30
2005-10	-1.04
2005-9	1.05
2005-8	0
2005-7	0.21
2005-6	0.95
2005-5	1.29
2005-4	-0.11
2005-3	-0.21

このデータを使って、リターン、月次標準偏差、年率標準偏差を求めてみましょう。

リターンは毎月のリターンに１を足して倍率に変換し、すべて掛け合わせます。

(1-0.0021)(1-0.0011)(1+0.0129)(1+0.0095),,,,,,(1+0.0071)(1+0.005)=1.0694

普通は、これを1/12乗して平均月次騰落率を求めます。

(1.0694)^^(1/12)＝1.005607　約　0.56%/月

年率平均騰落率（年リターン）を求めるには、１を足して倍率に変換し12乗すればよいです。

(1.005607)¹²＝1.0694　約　6.94%/年

今回、12個のデータを使ったので、最初の答えに戻りましたが、これは、計算が面倒なので、こういう例を使っただけです。

次に分散を計算します。
月次騰落率の算術平均を求め、それとの差（偏差）を毎月のデータごとに算出し、2乗します。
算術平均は単なる平均計算ですので、0.5642％とすぐに計算できます。
例えば、２００５年3月ですと、（-0.21-0.5642)²=-0.7742²=0.5993となります。

これを全部足し合わせると、8.3301になります。これをデータの数12個で割ると、月次の分散が求められます。

8.3301/12＝0.6942　：月次の分散

さらに、月次の分散の平方根（√）をとり、月次標準偏差　0.833（％）が得られます。

月次標準偏差と年次標準偏差の関係

前の章で、めでたく、標準偏差が求められました。
月次標準偏差　0.833（％）という数字から、年次の標準偏差に変換するにはどうすればいいのでしょうか?
一年は12ヶ月ですから、12倍すればいいのでしょうか?
いいえ、違います。√12倍すればいいのです。
ここでは、数学的な議論は省略しますが、「12倍するのは分散です。」
ですから、
月次標準偏差　0.833（％）→　2乗して分散　0.6942　→　12倍して年次の分散　8.3301　→　平方根（√）で年次標準偏差　2.8862%
結局、月次の標準偏差に√12倍した数字と同じになります。

ここで面白いことがわかります。
リターンは複利で増えますので、月次騰落率0.564%の12倍＝6.77よりも大きい6.94%のリターンになります。
それに対して、標準偏差は月次標準偏差0.833の√12倍（約3.464倍）＝2.886にしかなりません。
リターンを標準偏差で割ると月次では0.564/0.833=0.677ですが、年次ですと6.94/2.886=2.41になります。

勘のいい人はお分かりと思いますが、期間を長く見るほど、リターンとリスクの関係が改善するのです。

長期投資の優位性

ここで、保有されている方も多い、Man ADPを例に使って考察します。
Man ADPは、Man社の代表的なファンドですが、過去成績をみると、かなりのハイリターン（20.051%/年）をたたき出しています。
その分、リスクも高めで、標準偏差は18.287%です。

ここで、正規分布と標準偏差を思い出して欲しいのですが、±3倍の標準偏差（±3σ）以内に入る確率は99.73%（外れる確率は0.27%）になります。
普通考えると、極めて高い確率であると思われます。
そこで、横軸に投資後の経過年数をとり、縦軸にリターンをとったグラフを作ってみました。

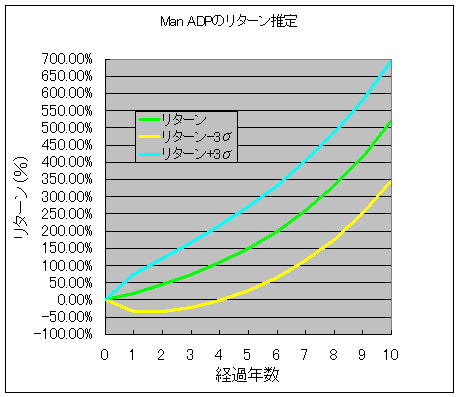
ここで示したのは、単純に、複利で計算してリターンと、±３σの線です。
リターンは、年々複利で増えていきますので、このようにどんどん上がっていきますが、リスク（標準偏差）は、2年たったからといって2倍になるのではなく、√2倍にしかなりません。
－３σという、かなり厳しい条件で見た場合、4年目までは、マイナスに転落していますが、その後プラスに転じ、10年経過後は350%のリターン（4.5倍）を得るとなっています。
これをみると長期投資の優位性が明らかだと思います。

もちろん、このシミュレーションは、今後も今までと同じような成績が続くとした場合です。
株式市場のように10年レベルで低迷したりすると、このようには行かなくなります。
ですので、長期投資だからいいというわけではなく、いろんな市場や戦略のファンドに分散することで、さらに、リスク分散を図る必要があるのです。
やっぱりここでも、「相関」を考慮した「アセットアロケーション」が重要であることは変わらぬ原理なのです。