ファンドの相関は、非常に大事な概念です。シャープレシオなど耳当たりのいい言葉もありますが、相関についての理解があってこそといっても過言ではありません。相関係数の算出過程の理解は非常に面倒なので、算数よりも雰囲気を重視した説明にしたいと思います。
相関(補足by.takumi)
自分が大雑把に解説している文章を以下抜粋。
身長と体重で、身長が高い人程体重が重いという仮定をたてた場合…平均身長と1人あたりの身長差が大きければ平均体重と1人あたりの体重差も大きくなるといえるでしょうか。
ならば、(身長ー平均身長)×(体重ー平均体重)の合計も大きくなる筈であるよ、と。
この場合、○○Cm・Kgという数字になるよ、と。ただ、この場合単位がぐちゃぐちゃなので、これのみで判断出来る数字じゃないよ、と。(普通の分散において、それを√としてはじめて単位が統一される事と同様)
非常にたくさんの人を対象にしてみると、ちょっと考えるとわかりますが、身長が高い人の方が体重が重いという関係があるでしょうから、
(身長ー平均身長)×(体重ー平均体重)ならば合計値がゼロになる事はないので普通に成り立つよ、と。((身長ー平均身長)の合計だと普通にゼロになってしまうので不可)(よって、2乗する)
ちなみに、(身長ー平均身長)×(体重ー平均体重)の合計がゼロにある場合も存在します。それは、身長と体重の関係が全く無関係という結果になる場合(相関ゼロ:無相関といいます)です。
非常に強引ですが、
A…160Cm 180Cm 200Cm B…160Kg 180Kg 200Kg
2つの相関性を調べると…
共分散=((身長ー平均身長)×(体重ー平均体重)の合計)/人数 =(20Cm*20Kg+0+20Cm*20Kg)/3人 =266.66…
A、Bとも標準偏差は…(20*20+20*20)/3のルートで、16,33…
相関係数=266,66…/16,33…*16.33…=1
※1=100%同じ
√2*√2=2というように、同じ標準偏差同士をかけあわせれば普通に分散という事に。身長ー平均身長の合計だとゼロになる為、2乗したものの合計を分散とするという定義より、AとBをかけあわせる事によりゼロにならないようにする、と。
<検証1>
Bを16.18.20Kgとした場合
Bの標準偏差は…1.63299‥ AとBの共分散は…(20*2+20*2)/3=26.66…
※単純に双方の数値が1/10となっただけなので結果は同じ
<検証2>
Bを32,36,40Kgとした場合
Bの標準偏差は…(4*4+4*4)/3、これをルートするから3.2659… AとBの共分散は…(20*4+20*4)/3=53.333…
※単純に双方の数字が上記の2倍となっているだけなので結果は同じ
要するに分散を平方根で元に戻したものが、標準偏差だよ、と。強引ですが標準偏差が同じものを2つかけあわしたら、普通にそれが分散だよ、と。偏差を合計したらゼロになるから、それを2乗してゼロにしないようにしたのが分散・標準偏差だよ、と。2つの数字(各偏差)をかけあわせた合計ならば、ゼロにはならないよ、と。
1つの数字の偏差の合計は常に必ずゼロになります。なので、2乗することによって、マイナスの数字をなくしちまって平均してやることで、偏差の平均の大小を表現しようとしたものが分散という考え方です。しかしこいつは、2乗しているので(%の2 乗)みたいな単位になっちゃって非常に使いづらいので、分散のルートを取って「標準偏差(%)」のように使いましょうと。
2つの数字(ここでは、身長と体重といったように2種類のという意味)の偏差をそれぞれ掛け算して平均すると何が出てくるか、、、、、これは、たくみさんが書いたように共分散というものです。
共分散は、2つの数字の相関を表す表現方法のひとつです。ですので、2つの数字の相関によっては、ゼロになることもありえます。 身長が160,180,200cmで、体重が200,180,160というときは以下のようになります。
(160-180)(200-180)+(180-180)(180-180)+(200-180)(160-180)=-400+0+-400=-800
上式を人数=3で割ると-266.66,,,,ということで2つの数字が負の共分散を持ちます。こいつは、片方が大きいとき、もう片方が小さくなる状態ですね。
次に、身長が160,180,200cmで、体重が180,180,180というときを考えて見ましょう。
(160-180)(180-180)+(180-180)(180-180)+(200-180)(180-180)=0+0+0=0
上式が0ということで2つの数字の共分散はゼロになります。こいつは、片方が大きくても、小さくても、もう片方が関係しない状態ですね。
身長と体重ならばなんとなく相関はありそうですが、コンビニの客の身長と買い物した金額などというものはカナ~リ相関なさそうですよね。2つの数字の偏差の掛け算を平均するとゼロになることがあり、それは、相関係数が0になるとき=無相関ということです。 (by TONE)
ン~、ホント完全な理解ではないですが、大まかになんとか意味が分かりました。はい、雑学的の本の説明で「ほ~、なる程」となりやした。
基本的に自分は大学はモロ文系でした。当然、大学にいっている間は数学は一般教養ですらやってません。で、社会に出てからも数字を使う機会は殆どありませんでした。(小難しい計算、という意味で)
で、流れ流れにコンサルの仕事をするようになり、自分の人生にゃ数学は特に使う事もないであろうと思っていたのが一転、モロ数学知識が必要となり、、高校時代の参考書などを引っ張り出したりしてヒーコラいっていた記憶が。恐らくそんな自分だからこそ、書ける初歩的な事もあるでしょうから、「え??」というような初歩的な事の補足、ザっとしてみます。まずは相関係数の理解について。
相関係数0.32、と出ていたら頭が痛くなる人、実際いるような気します(笑)
* 1から1までの間に収まる、というので「なんでやねん?」と思う人もいるでしょう。ここは、パーセントに置き換えると理解しやすくなります。
* 100%から100%までの間に収まる。 相関係数0.32なら、32%同じ動きする、と。
100%同じ動きする=相関性1.0
0%同じ動きする=全く相関性がない
ね?なんか0.32とかいう数字で見るより理解出来る気しません??(自分はこう置き換えて最初は「なるほど」と納得してました)
以上、補足でした。(by.takumi)
相関とは
一般的に相関は強弱で表現されます。強い相関、弱い相関といった具合です。ファンド投資における相関とは、あるファンドAが5%価格が上昇したときにBも5%価格が上昇し、常に、同じような値動きをする場合、「AとBの間には極めて強い正の相関がある」といえます。完全に値動きが一致する場合は、相間係数が1になり、完全に同期している状態をあらわします。
逆に、ファンドAが5%上昇すると、ファンドBが5%下降するといった具合に全く逆の動きをする場合、「AとBの間には極めて強い負の相関がある」といいます。完全に逆の動きをする場合相関係数は-1になります。
また、Aの動きとBの動きが完全にばらばらで、Aが上がるからといってBが上がるわけでも下がるわけでもなく、そのときによってバラバラという状態では、AとBの相関は弱いといいます。完全にバラバラならば、「無相関」ということになり、相関係数は0になります。
このように、AとBの動き方についての関係を表現したものを相関といい、相関係数は-1~0~1の範囲をとります。
ファンドの値動きに対する相関を考える時、いくつかのファンドがあると、総当りで全ての組み合わせの相関係数が存在します。
たとえば、A,B,Cの3つのファンドがあるときに、ファンド間の相関というと、
AとBの相関、AとCの相関、BとCの相関
といった具合になります。
もうおわかりの様に、ファンドの数が増えると相関係数の数も急激に増えます。行列計算をイメージしていただければ良いと思います。
相関のイメージ
それでは、実際のファンドの値動きを使って相関のイメージをつかみましょう。
ここでは、AIITの3つのファンドを使って、簡単に表現してみます。
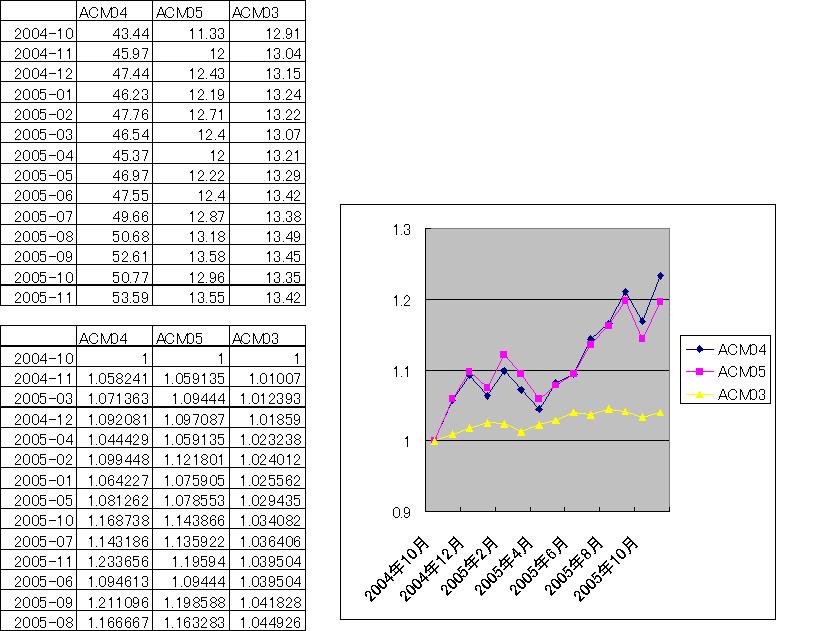
基準のファンドはAIIT_ACM04 Global Growth Trendsというファンドにします。全世界の成長株に投資するファンドです。
比較の1番目は非常に基準のファンドとの相関係数が高いAIIT_ACM05 Global Value Portfolioです。相関係数は0.9724と極めて高い正の相関があります。このファンドも株式に投資するファンドです。
比較の2番目は逆に相関係数が小さいAIIT_ACM03 Global Bond Portfolioです。これは、債券ファンドで、さすがに株式ファンド同士と比べると相関係数が低くなっており、0.2738です。
そのままの価格では、比較し難いので、2004年10月時点の価格を1としてプロットしました。
これを見れば、多くを語る必要は無いですね。AIIT_ACM04 Global Growth TrendsとAIIT_ACM05 Global Value Portfolioはほとんど同じ値動きを示しています。大雑把に言えば、同じファンドだといっても良いぐらいです。
それに対して、債券ファンドであるAIIT_ACM03 Global Bond Portfolioは上記2つとは違う動きを示しています。